As a relatively new teacher (partway through my third year), I’ve already gone through many paradigm shifts and revelations related to how I design learning experiences. After years served in many educational institutions, I’ve had plenty of time to reflect on how I learn best; one could even say that I am an expert in the field. But it wasn’t enough when I was trying to create learning experiences from the teacher’s perspective. Unfortunately, knowing how I learned best did not translate to designing good learning experiences.

But why? To answer this, I thank Peter Liljedahl for a quote shared during a Pro-D event at my school: “We are the survivors.” Peter explained that we (educators) are not representative of our students. We’ve survived many trials over many more years in academia and we are the ones that came out on top. On the other hand, our students are at the beginning of this journey and many may not reach the same level we did. Essentially, what worked for us (the survivors) may not work for our students. Internal knowledge of our individual learning processes is not enough to design good learning experiences. Below, I will chronicle how my understanding of learning design has shifted to better fit current themes and ideas in modern education.
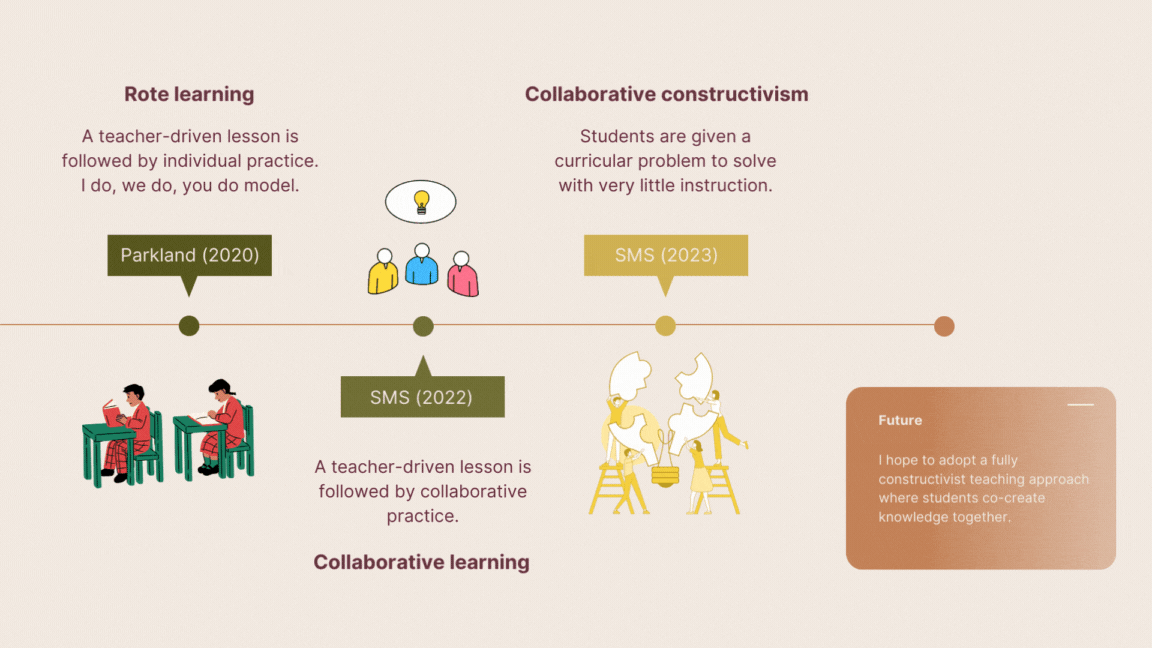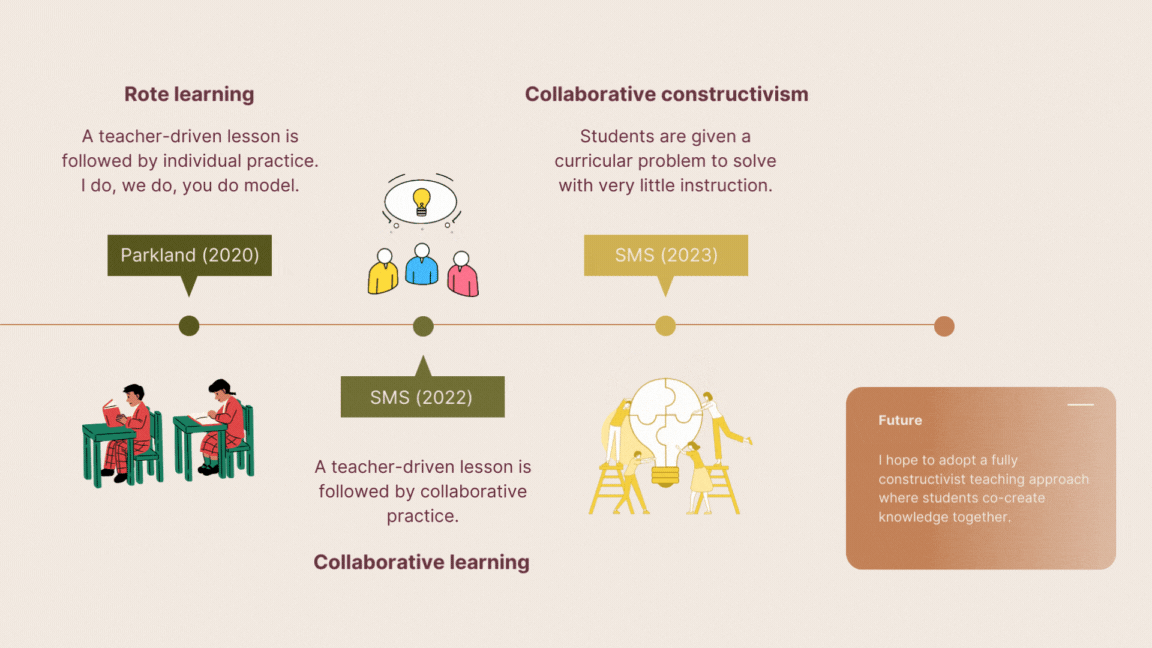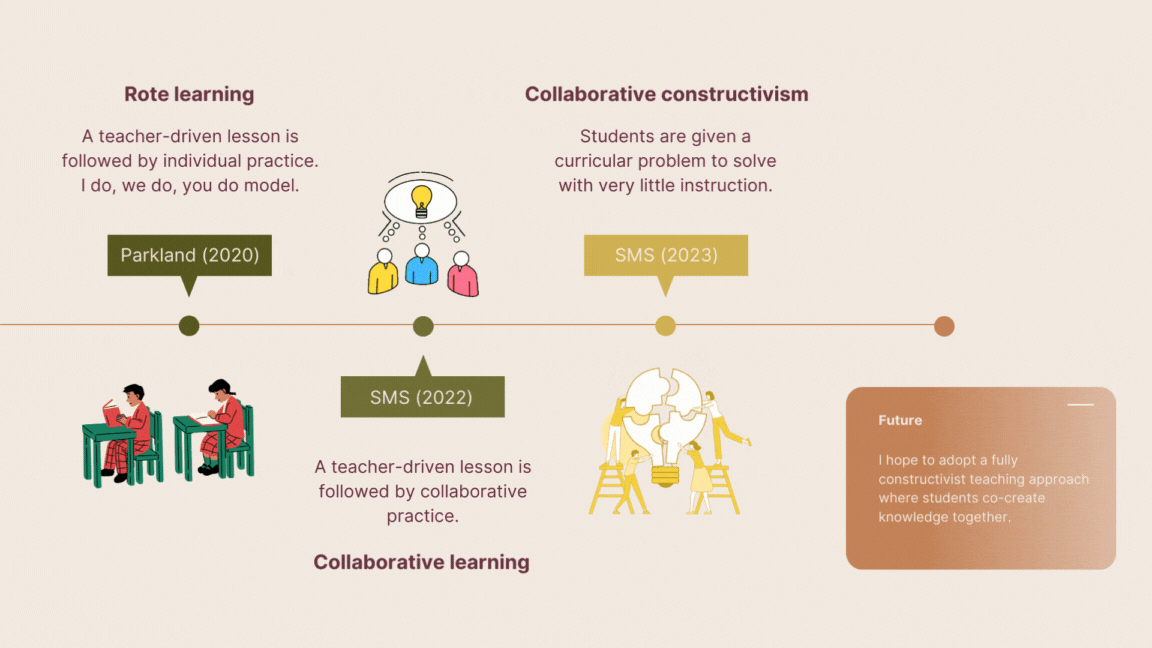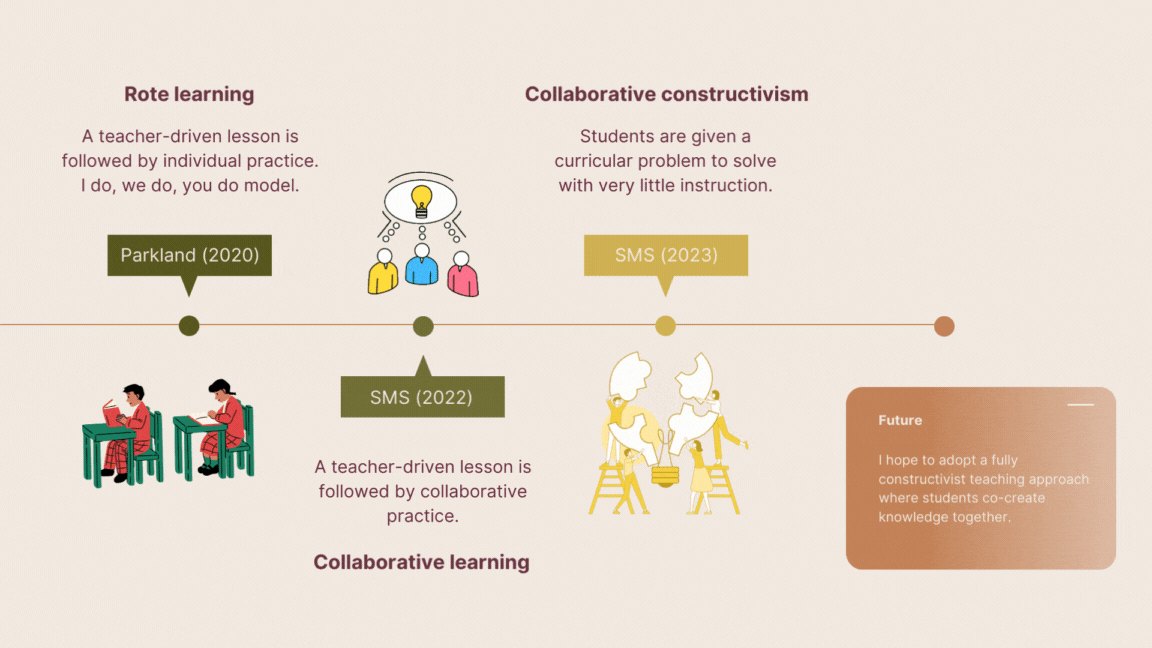
In the beginning, I was trained in the old ways. Stand, deliver, practice, test. This seemed perfectly reasonable to me since this is how I was taught. What I realized later was that this is not how I learned. Caught in an endless loop of cramming and regurgitation, I propagated learning designs that didn’t work for me or my students. This is apparent in hindsight but quite evasive in practice for two reasons: (a) this is how students like to “learn” and (b) the test results are usually very high. This is because the typical cycles in traditional math classrooms are easy to game; lecture, practice, test, rinse, repeat. These cycles usually take three weeks and include a practice test similar to the actual test. I wonder why our students are so successful learning in this way?! There is one issue with this learning design; our students become abysmal problem solvers.

My first mentor teacher, a wiley old physics expert, once said: “There is no such thing as an educational emergency.” For a long time, I lived by these words and defended them with my life. He was a relaxed guy and so was I; this phrase gave me serenity when teaching life got hectic. To be pedantic, I still mostly agree with him. Most emergencies are not educational: they are health-related (and happening at school) or social (because of youth). What shook my faith was realizing that my students could not solve problems. Now that was an educational emergency.
As the late, great Thomas Kuhn prophesied: a paradigm shift occurs when a field (or discipline) is in crisis. We, my friends, were in crisis. What is the point of teaching math to kids if it isn’t making them better problem-solvers? Even as a math teacher trying to justify their existence, I recognize that many of my students won’t study math after leaving my classroom. So then, we must break the glass on the metaphorical fire extinguisher box and begin triage. The first question was obvious: “How do I make my students better problem-solvers.” The answer was even easier: get them to solve problems. For this, I turned again to Peter Liljedahl.
The cookbook was simple:
- Get them standing up
- Get them into small groups
- Put them in front of verticle whiteboards
- Give them a problem
At no point in the method above do I “teach” them anything. Everything that they use in this space they either already know or they’ve created together. The distinct learning design at play here is constructivism. Many of my students already possess the prerequisite skills to build solutions to problems for themselves. This shifts my role from synthesizing and summarizing textbook information to generating questions. Just yesterday, we explored geometric sequences; a typical lesson would start with a definition or formula, a worked example, and then some seatwork. The formula for a geometric sequence is given below:
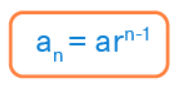
Alternatively, I could give students a series of numbers and ask them a few questions:
2, 4, 8…
- What are the next three numbers in the pattern?
- How are the numbers changing?
- What is the 100th number?
This alternative method doesn’t require any explanation of jargon or terminology. It also doesn’t necessitate a formal explanation of geometric sequences. My students can recognize patterns and multiply. This new approach is all about giving access points to new problems that rely on already solidified knowledge. The other benefit is social; each student brings a unique blend of knowledge and skill to their group. Given sufficient time and a reduction of social barriers, all of the groups were able to successfully complete the task. Astonishingly, about half of the groups formed an algebraic statement similar to the one above. And for those that didn’t, I directed them to a whiteboard with students that did.

Learning design is not about creating the perfect lesson, it is about asking the perfect question.
An interesting note: when searching for a featured image for this post, almost every image or photograph placed an adult at the center of the learning experience with children or youth listening.